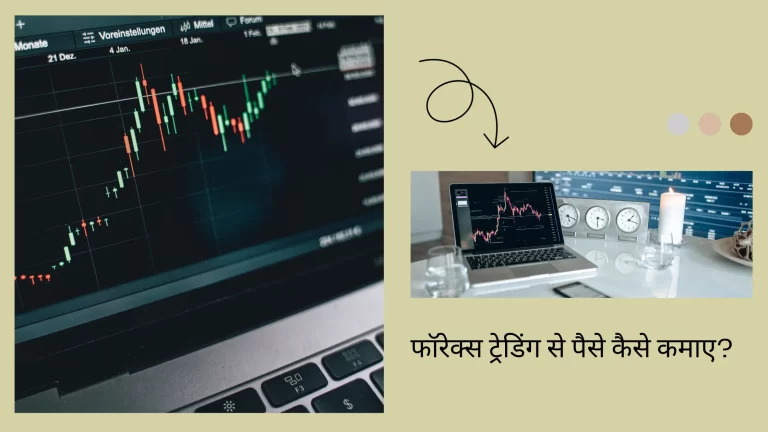
फॉरेक्स ट्रेडिंग से पैसे कैसे कमाए? | Forex trading se paise kaise kamaye?
“फॉरेक्स ट्रेडिंग से पैसे कैसे कमा…

“फॉरेक्स ट्रेडिंग से पैसे कैसे कमा…

यदि आप विदेशी मुद्रा (फॉरेक्स) के माध्यम…

भारतीय सेना, वायु सेना और नौसेना के लिए …

GM’s most recent bid to increase U.S. EV deals and outperform rival Tesla is a $30,000 all-electric SUV pointed decisively at the mass market. The 2024 Chevrolet Equinox EV, which will come in LT and RS models and has an expected…

Hdfc Regalia Credit Card भारत में सबसे अ…
भारतीय स्टेट बैंक (एसबीआई) ने महिला बाजा…
क्या आपने कभी कोई बुरा सपना देखा है जिसम…

Starting a business is not an easy task and finding a perfect Luxury names for Business is even harder only if you lack certain naming ideas. Additionally, Business owners and Enterprenurs put their maximum focus in detemining the fate of their…